面白いので更に続けてみましょうw
前回は無限等比級数の和を簡単に説明いたしました。
今回は「じゃあ有限の場合は?」を考えてみましょう。
前回の例では、50回ぐらいの繰り返しでEXCEL上では誤差がなくなったので、
単純に前回の表を作って求めても良いとは思います。
ましてやセット物じゃなくてリミッターがある場合などは特に。
ただそれだと話が終わっちゃいますので、こういう公式もあるんだなと、なんとなく
感じていただけたらと。
では前回の確変突入・継続率60%で考えてみましょう。
10回リミッターだとしたら(初回を含めて)・・・
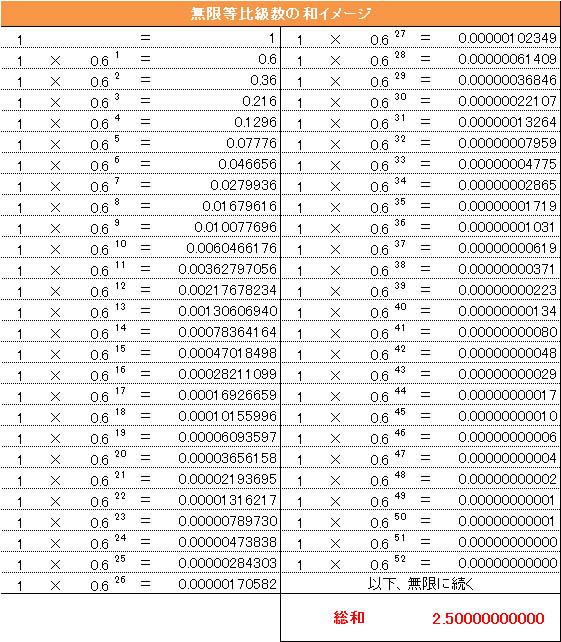
上記表の 「0.69」までの値を総和すれば求められますね。
簡略化して計算すると
1+0.6+0.62+0.63+0.64+0.65+0.66+0.67+0.68+0.69≒2.484883456
リミッターが無ければ2.5回になりますが、リミッターがあるおかげで
約2.485回になるわけですが、体感では誤差に等しい程度の値ですね。
この数式は、前回の考え方と全く同じですが、有限なのでそこが少し変わるだけですね。
10回リミットと考えた場合(経過は前回と同じなので省略しています)
S = a +ar + ar2 + ar3 + ar4 ・・・・・・+ ar9
- Sr =ar + ar2 + ar3 + ar4 ・・・・・・+ ar9 + ar10
--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
S-Sr = a - ar10
下記のようになりました。
S-Sr = a-ar10
これをSを求める式に変形すると
S=a(1-r10)÷(1-r)
となります。
さっそく計算してみましょう。
a=1
r=0.6
とすると
1×(1-0.610)÷(1-0.6)≒2.484883456
先ほど求めた
1+0.6+0.62+0.63+0.64+0.65+0.66+0.67+0.68+0.69≒2.484883456
同値になりました^^
以上です。
前回は無限等比級数の和を簡単に説明いたしました。
今回は「じゃあ有限の場合は?」を考えてみましょう。
前回の例では、50回ぐらいの繰り返しでEXCEL上では誤差がなくなったので、
単純に前回の表を作って求めても良いとは思います。
ましてやセット物じゃなくてリミッターがある場合などは特に。
ただそれだと話が終わっちゃいますので、こういう公式もあるんだなと、なんとなく
感じていただけたらと。
では前回の確変突入・継続率60%で考えてみましょう。
10回リミッターだとしたら(初回を含めて)・・・

上記表の 「0.69」までの値を総和すれば求められますね。
簡略化して計算すると
1+0.6+0.62+0.63+0.64+0.65+0.66+0.67+0.68+0.69≒2.484883456
リミッターが無ければ2.5回になりますが、リミッターがあるおかげで
約2.485回になるわけですが、体感では誤差に等しい程度の値ですね。
この数式は、前回の考え方と全く同じですが、有限なのでそこが少し変わるだけですね。
10回リミットと考えた場合(経過は前回と同じなので省略しています)
S = a +
- Sr =
--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
S-Sr = a - ar10
下記のようになりました。
S-Sr = a-ar10
これをSを求める式に変形すると
S=a(1-r10)÷(1-r)
となります。
さっそく計算してみましょう。
a=1
r=0.6
とすると
1×(1-0.610)÷(1-0.6)≒2.484883456
先ほど求めた
1+0.6+0.62+0.63+0.64+0.65+0.66+0.67+0.68+0.69≒2.484883456
同値になりました^^
以上です。
