ちなみにCR海物語3のMNRSは、リミット100回を無視すれば、
0.00518672199170124(M)×15(N)×10(R)×15(S)=11.6701244813278 ぐらいですw
さてタイトルの件ですね。
これ実は非常に単純なんです。
言葉で説明すると(確変突入・継続率60%とします)
まず初当たりで大当り回数1回。
で、確変を引く可能性が60%ですから初当たり1回プラス大当り回数0.6回。
更に確変が続く可能性が、0.6×0.6=0.36 上記プラス大当り回数0.36回。
更に更に確変が続く可能性は、0.6×0.6×0.6=0.216 上記プラス大当り回数0.216回
これを無限に繰り返して、大当り回数を総和するだけなんですね。
これを式にすると
1 + 0.6 + 0.62 + 0.63 + 0.64 +・・・・・・・
これを 初項1 公比0.6 の無限等比級数の和 と言います。
わかりやすく言いますと、初項は始まりの値。公比は繰り返す値。
そしてとりあえず表にしてみましたw
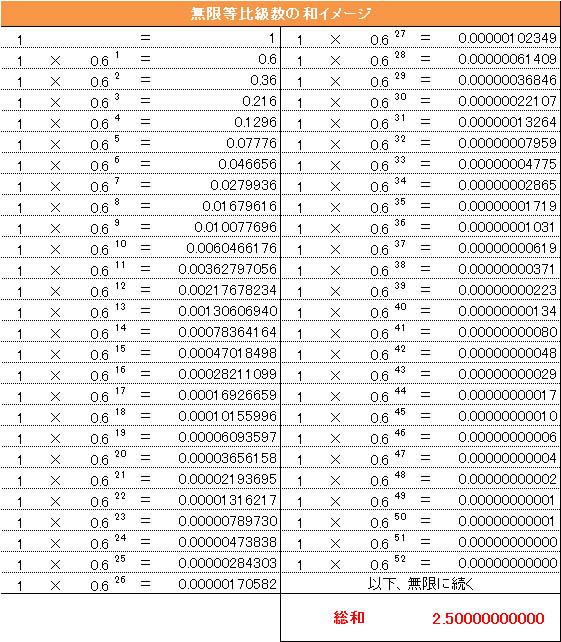
本当は無限に繰り返さなければならないのですが、表のように52回も確変が継続すると
(初回当たりを含めると53連チャン)、EXCELでも誤差が無くなります。
こうやって計算する事も出来ますが、タイトル通りの計算式
1÷(1-0.6)=2.5
だと一発ですね^^
なぜこの式で求める事が出来るのでしょうか?
これは無限等比級数の和と言われる計算式です。
初項a 公比r を無限に総和する公式が下記になります。
a÷(1-r) ※但し1 < |r| < 1
ここで一般化しますが、一気に難しく感じるのは気のせいですよ^^
先ほどの 1+0.6+0.62+0.63+・・・・を一般化すると
※先ほどは初項(今回の場合は初当たりである1)を乗算するのを省略していましたが
S = a + ar + ar2 + ar3 + ・・・・・・+ arn-1 + arn ・・・・・・・・①
こうなります。
ぶっちゃけ今回は a が1で r が0.6ですよね^^
一般化するとなんか凄く数学しているイメージがありますが、実際はただの算数ですw
ここで式を整理するために、両辺に r を乗算します。
まあ、累乗の数が1増える感じですね。すると
Sr = ar + ar2 + ar3 + ar4 + ・・・・・・+ arn-1 + arn ・・・・・・・・②
ここで式を整理します。
①-②します。
S = a + ar + ar2 + ar3 + ar4 ・・・・・・+ arn-1 + arn
- Sr = ar + ar2 + ar3 + ar4 ・・・・・・+ arn-1 + arn
--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
こうやって式を見ると分かると思うのですが、右辺は a より右側を全て消す事が出来ます。
S = a +ar + ar2 + ar3 + ar4 ・・・・・・+ arn-1 + arn
- Sr =ar + ar2 + ar3 + ar4 ・・・・・・+ arn-1 + arn
--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
S-Sr = a
「S-Sr = a」 と整理する事が出来ましたね^^
ここからaとrからSを求める式に変形して
S=a÷(1-r)となります。
変形前の S-Sr = a が本当に正しいのか?
これが間違っていたらなんにもなりませんw
aは1だとわかっていますが、実際にこの式でaが1になるか計算してみましょう。
S=2.5
r=0.6
2.5 - 2.5 × 0.6 = 2.5 - 1.5 = 1
以上です。
0.00518672199170124(M)×15(N)×10(R)×15(S)=11.6701244813278 ぐらいですw
さてタイトルの件ですね。
これ実は非常に単純なんです。
言葉で説明すると(確変突入・継続率60%とします)
まず初当たりで大当り回数1回。
で、確変を引く可能性が60%ですから初当たり1回プラス大当り回数0.6回。
更に確変が続く可能性が、0.6×0.6=0.36 上記プラス大当り回数0.36回。
更に更に確変が続く可能性は、0.6×0.6×0.6=0.216 上記プラス大当り回数0.216回
これを無限に繰り返して、大当り回数を総和するだけなんですね。
これを式にすると
1 + 0.6 + 0.62 + 0.63 + 0.64 +・・・・・・・
これを 初項1 公比0.6 の無限等比級数の和 と言います。
わかりやすく言いますと、初項は始まりの値。公比は繰り返す値。
そしてとりあえず表にしてみましたw

本当は無限に繰り返さなければならないのですが、表のように52回も確変が継続すると
(初回当たりを含めると53連チャン)、EXCELでも誤差が無くなります。
こうやって計算する事も出来ますが、タイトル通りの計算式
1÷(1-0.6)=2.5
だと一発ですね^^
なぜこの式で求める事が出来るのでしょうか?
これは無限等比級数の和と言われる計算式です。
初項a 公比r を無限に総和する公式が下記になります。
a÷(1-r) ※但し1 < |r| < 1
ここで一般化しますが、一気に難しく感じるのは気のせいですよ^^
先ほどの 1+0.6+0.62+0.63+・・・・を一般化すると
※先ほどは初項(今回の場合は初当たりである1)を乗算するのを省略していましたが
S = a + ar + ar2 + ar3 + ・・・・・・+ arn-1 + arn ・・・・・・・・①
こうなります。
ぶっちゃけ今回は a が1で r が0.6ですよね^^
一般化するとなんか凄く数学しているイメージがありますが、実際はただの算数ですw
ここで式を整理するために、両辺に r を乗算します。
まあ、累乗の数が1増える感じですね。すると
Sr = ar + ar2 + ar3 + ar4 + ・・・・・・+ arn-1 + arn ・・・・・・・・②
ここで式を整理します。
①-②します。
S = a + ar + ar2 + ar3 + ar4 ・・・・・・+ arn-1 + arn
- Sr = ar + ar2 + ar3 + ar4 ・・・・・・+ arn-1 + arn
--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
こうやって式を見ると分かると思うのですが、右辺は a より右側を全て消す事が出来ます。
S = a +
- Sr =
--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
S-Sr = a
「S-Sr = a」 と整理する事が出来ましたね^^
ここからaとrからSを求める式に変形して
S=a÷(1-r)となります。
変形前の S-Sr = a が本当に正しいのか?
これが間違っていたらなんにもなりませんw
aは1だとわかっていますが、実際にこの式でaが1になるか計算してみましょう。
S=2.5
r=0.6
2.5 - 2.5 × 0.6 = 2.5 - 1.5 = 1
以上です。
